<blink><b><font color="red">Logaritma Natural, Bilangan Euler, Beserta Turunan dan Integralnya</font></b></blink>

Logaritma natural adalah logaritma yang berbasis e, dimana e adalah 2.718281828459... (dan seterusnya). Logaritma natural terdefinisikan untuk semua bilangan real positif x dan dapat juga didefinisikan untuk bilangan kompleks yang bukan 0.

Ahli matematika biasanya menggunakan "ln(x)" atau "log(x)" untuk menotasikan log_e(x), atau logaritma natural dari x, dan menggunakan "log₁₀(x)" untuk menotasikan logaritma berbasis 10 dari x.

Insinyur, ahli biologi, dan orang dalam bidang-bidang lain, hanya menggunakan "ln(x)" atau kadang-kadang (untuk supaya lebih jelas) "log_e(x)" untuk menotasikan logaritma natural dari x, dan "log(x)" digunakan untuk logaritma berbasis 10, log₁₀(x) atau, dalam konteks teknik komputer, log₂(x).

Kebanyakan bahasa komputer, termasuk C, C++, Fortran, dan BASIC, "log" atau "LOG" berarti logaritma natural.

Pada kalkulator, tombol ln berarti logaritma natural, sedangkan tombol log adalah untuk logaritma berbasis 10.

Ln sebagai invers fungsi eksponensial natural

Fungsi ln adalah invers dari fungsi eksponensial:

$\ e^{\ln(x)} = x \,\!$ untuk semua x yang positif dan

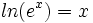$\ ln(e^x) = x \,\!$ untuk semua x yang real.

Logaritma dapat didefinisikan untuk basis lainnya, asal positif, tidak hanya e, dan biasanya berguna untuk memecahkan persamaan yang variabel tidak diketahuinya merupakan pangkat dari variabel lain.

Mengapa disebut "natural"

Sekilas, tampaknya yang lebih "natural" tentunya adalah logaritma yang berbasis 10, karena basis angka yang digunakan umumnya juga 10. Namun, ada dua alasan mengapa ln(x) disebut logaritma natural: pertama, persamaan-persamaan yang variable tak diketahuinya merupakan pangkat dari e jauh lebih sering dijumpai dibanding yang merupakan pangkat dari 10 (karena sifat-sifat "natural" dari fungsi eksponensial yang dapat menggambarkan growth/pertumbuhan dan decay/penurunan), dan kedua, karena logaritma natural dapat didefinisikan dengan mudah menggunakan integral yang dasar atau Deret Taylor (lihat penjelasan di bawah), dan logaritma berbasis lainnya tidak dapat didefinisikan seperti ini.

Sebagai contoh, lihat turunan dibawah ini:

$\frac{d}{dx}\log_b(x) =\frac{1}{x \cdot \ln b}$

Jika basis b adalah e maka turunan yang didapat adalah 1/x dan jika x=1, kemiringan kurva adalah 1.

Definisi

Secara formal, ln(a) dapat didefinisikan sebagai luas dibawah grafik (integral) dari 1/x dihitung dari 1 ke a, atau,

$\ ln(a)=\int_1^a \frac{1}{x}\,dx.$

Definisi tersebut mendefinisikan suatu logaritma, karena memenuhi sifat fundamental logaritma, yaitu:

$\ ln(ab)=\ln(a)+\ln(b) \,\!$

Ini dapat ditunjukkan dengan mendefinisikan $φ(t) = a t$ dan dengan menggunakan rumus substitusi:

$\ln (ab) = \int_1^{ab} \frac{1}{x} \; dx = \int_1^a \frac{1}{x} \; dx \; + \int_a^{ab} \frac{1}{x} \; dx =\int_1^{a} \frac{1}{x} \; dx \; + \int_1^{b} \frac{1}{t} \; dt = \ln (a) + \ln (b)$

Bilangan e, selanjutnya dapat didefinisikan sebagai bilangan real yang unik a dimana $ln(a) = 1$ .

Kenapa turunan e^x adalah e^x juga

Pertanyaan yang bagus, saya sendiri juga baru kepikiran kenapa begitu ya? Dalam buku-buku kalkulus hanya dikatakan $\frac{d}{dx}e^{x}=e^{x}$ tanpa ada penjelasannya.

Okey akan saya coba membuktikannya, pertama-tama akan saya buktikan dengan menggunakan definisi dari turunan/derivative. yaitu

$\underset{h\rightarrow0}{Lim}\frac{f(x+h)-f(x)}{h}$

Jadi kita peroleh

$\underset{h\rightarrow0}{Lim}\frac{e^{(x+h)}-e^{x}}{h}$

$\underset{h\rightarrow0}{Lim}\frac{e^{x}e^{h}-e^{x}}{h}$

$\underset{h\rightarrow0}{Lim}\frac{e^{x}(e^{h}-1)}{h}$

….

Saya mulai bingung nich, soalnya kalo diterusin hasilnya adalah nol. Mm..apa yang salah yach?? Gimana kalo kita ganti metode aja. Gamana kalo kita menggunakan definisi dari $e^x$ aja. Yaitu:

$e^{x}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\ldots$

diperoleh

${\displaystyle \frac{d}{dx}e^{x}=\frac{d}{dx}(1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\ldots})$

$=0+1+\frac{2x}{2!}+\frac{3x^{2}}{3!}+\frac{4x^{3}}{4!}+\ldots$

${\displaystyle =1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\ldots})$

$=e^{x}$

Oalah..tenyata cuman muter-muter , mbolak-mbalik aja to…

Bukti Turunan Pake Logaritma

math brain

Berikut adalah rumus-rumus dasar turunan/ derivatif:

Kalau Tulisan Rumusnya Kurang Jelas Silahkan diCopy-Paste Aja

Bila y=f(x) , y’=f’(x), dan a adalah konstanta maka:

1.
2.
3.
4.

5.
6.	etc…

Lihat lanjutan post di bawah untuk mengetahui bukti-buktinya.
=========================================================================

Mengapa Turunan dari

adalah

?? (a konstanta)

Bukti ini sangat mudah. Langsung kita gunakan definisi dari derivatif.
(atau bisa kita gunakan cara seperti di post “bukti sifat-sifat turunan” yang dilakukan secara bertahap..)
.

TERBUKTI

Selanjutnya: Mengapa turunan dari

adalah

Kita bisa saja menguraikan penurunan rumus ini dari awal, seperti cara yang serupa seperti di atas. Namun, kita gunakan saja rumus sebelumnya, untuk membuktikan rumus ini., supaya kita tidak 2 kali kerja..

Di atas merupakah rumus yang sudah kita dapatkan sebelumnya. Substitusikan a=e.

Ingat bahwa ln e =1. Ingat bahwa: = , maka:

TERBUKTI

=========================================================================

Mengapa turunan dari

adalah

ln-kan kedua ruas.

turunkan kedua ruas. Ingat bahwa turunan dari ln x adalah 1/x.

TERBUKTI

=========================================================================

Mengapa turunan dari

adalah

?? (a konstanta)

ln-kan kedua ruas.

turunkan kedua ruas, maka hasilnya:

TERBUKTI

Selanjutnya: Mengapa turunan dari

adalah

Sesuai dengan rumus sebelumnya:

Jika a=e, maka:

TERBUKTI

=========================================================================

Mengapa turunan dari

adalah

Untuk membuktikan ini, kita bisa gunakan definisi awal dari derivatif.
.

Ingat bahwa:
==> Note: rumus di atas HARUS dapat diturunkan sendiri.
Dengan demikian, persamaan menjadi:

TERBUKTI

Mengapa turunan dari

adalah

Pembuktiannya menggunakan cara yang sama seperti di atas.

Ingat bahwa:
==> rumus di atas HARUS bisa diturunkan sendiri.
Dengan demikian, persamaan menjadi:

TERBUKTI

Note: Cara lain menurunkan turunan sin x dan cos x yaitu dengan melihat identitas eulernya (Lihat di sini):
*)
*)
Dengan menurunkan sisi ruas kanan dari , maka akan menghasilkan sisi kanan dari .

Mengapa turunan dari

adalah

Fungsi tangen dapat dibentuk ke dalam bentuk pembagian.

Kemudian, ingatlah sifat turunan berikut.

Dengan menggunakan sifat itu, maka pembuktian turunan f(x) akan segera terbukti.

TERBUKTI

Rumus-rumus di atas adalah rumus turunan yang siap pakai. Selanjutnya, akan dibahas pembuktian untuk rumus-rumus yang kurang begitu *terpakai*. Jika terpakai pun, kita dapat dengan mudah menurunkannya. Konsep menurunkannya sama seperti di atas, kecuali adanya beberapa yang mengharuskan substitusi trigonometri.. But, lagi-lagi, rumus di bawah jangan sengaja dihapal (kecuali kalau tidak sengaja terhapal).. ;P

Bukti: turunan dari

, dan

Bukti bisa menggunakan teorema sebelumnya yang berbunyi: .
Sama halnya seperti menggunakan dalil rantai…

Dengan aturan rantai, maka:

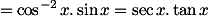
TERBUKTI

Bukti turunan dari fungsi arcsin x, arccos x, arctan x, etc

Tidak semua bukti akan diberikan di sini, karena prosesnya hampir sama. Dan, akan terlalu banyak jika semuanya dibahas dalam satu post di blog. So, it is your challenge to prove it by yourself…

Bukti turunan dari fungsi arcsin x

y= arc sin x

sin y = x

Turunkan kedua ruas, maka hasilnya:

cos y.dy = dx

Dengan menggambar segitiga siku-siku dengan sudut y (memisalkan sisi depan adalah x, sisi miring 1), maka kita akan mendapatkan cos y. (Lihat gambar)

Atau, kita bisa memanfaatkan identitas trigonometri: , maka:
.

Di sini, kita dapat: . Maka, tinggal disubstitusikan…

TERBUKTI

Bukti turunan dari fungsi arccotan x

Turunkan kedua ruas maka hasilnya:

, maka

.
Gambarkan segitiga siku-siku dengan sudut y. Misalkan sisi depan adalah 1, dan sisi samping adalah x. (lihat gambar).

Dengan demikian, kita bisa menghitung panjang sisi miring, kemudian menghitung nilai dari sin y.

Substitusikan nilai dari sin y ke persamaan sebelumnya.

TERBUKTI

Bukti turunan dari fungsi hiperbolik: sinh x, cosh x, etc

Pembuktiannya menggunakan sisi kanan dari identitas terhadap euler. Ingat bahwa:

Bukti turunan sinh x

(TERBUKTI)

Bukti turunan cosh x
(TERBUKTI)

Bukti turunan tanh x

___________ (TERBUKTI)

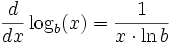
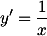
4 Responses So Far:

Unknown mengatakan...: isinya bagus...
tapi suer, namanya itu ganggu banget.... bikin kesel... ngikutin kemana-mana....
at least thanx a lot...
(^-^); Reply 14 September 2010 pukul 18.33
Agung Dwi Prasetyo mengatakan...: yeah, terimakasih atas masukan anda.....
sy akan cba mmprbaikinya.....
thanks....; Reply 19 September 2010 pukul 14.39
Agus S mengatakan...: Mantap bro berguna banget buat yang lagi mempelajari logaritma natural yang sangat membingungkan itu,hehehe....; Reply 28 Oktober 2010 pukul 09.17
Unknown mengatakan...: Ampuun prof.; Reply 12 Mei 2014 pukul 00.28

HardCode

Logaritma Natural, Bilangan Euler, Beserta Turunan dan Integralnya 4

Mengapa disebut "natural"

Definisi

Kenapa turunan e^x adalah e^x juga

Bukti Turunan Pake Logaritma

4 Responses So Far:

Categories

Archives

Follower

About Me